Mathematical and Computational Nonlinear Physics
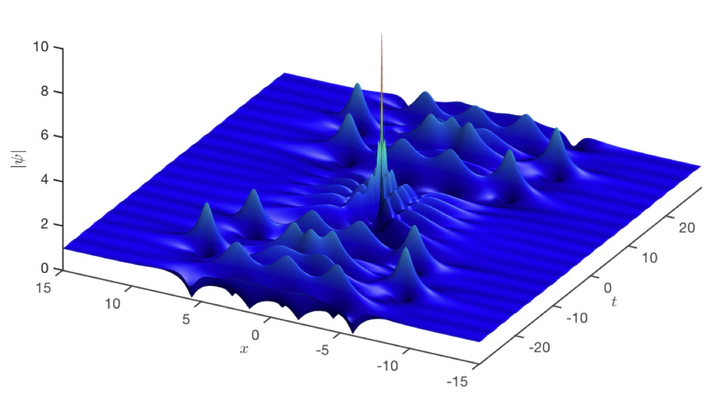A fifth order quasi-rogue wave solution of the cubic nonlinear Schrödinger equation.Sample Projects
Deriving the Lax pair for the Hirota and Quintic nonlinear Schrödinger equations.
Studying the Fermi-Pasta-Ulam-Tsingou reccurence in the nonlinear Schrödinger equation.
Deriving doubly-periodic “Nonlinear Talbot Carpet” solutions and their possible applications in nonlinear optics.
Developing an experimentally feasible method for the systematic generation of higher-order breather solutions.
Sole developer and maintainer of the Julia package
NonlinearSchrodinger.jl, implementing a variety of numerical algorithms and the Darboux transformation for the classically integrable nonlinear Schrödinger equation. [GitHub]
Relevant Publications and Preprints
(2022).
Higher-order breathers as quasi-rogue waves on a periodic background.
Nonlinear Dynamics.
(2021).
NonlinearSchrodinger: Higher-Order Algorithms and Darboux Transformations for Nonlinear Schrödinger Equations.
arXiv.
(2022).
On different aspects of the optical rogue waves nature.
Nonlinear Dynamics.
(2022).
Multi-elliptic rogue wave clusters of the nonlinear Schrödinger equation on different backgrounds.
Nonlinear Dynamics.
(2019).
Breathers, solitons and rogue waves of the quintic nonlinear Schrödinger equation on various backgrounds.
Nonlinear Dynamics.
(2019).
Talbot carpets by rogue waves of extended nonlinear Schrödinger equations.
Nonlinear Dynamics.
(2015).
Anatomy of the Akhmediev breather: cascading instability, first formation time, and Fermi-Pasta-Ulam recurrence.
Physical Review E.
(2016).
Maximal intensity higher-order Akhmediev breathers of the nonlinear Schrödinger equation and their systematic generation.
Physics Letters A.
(2017).
Peak-height formula for higher-order breathers of the nonlinear Schrödinger equation on non-uniform backgrounds.
Physical Review E.
(2017).
Systematic generation of higher-order solitons and breathers of the Hirota equation on different backgrounds.
Nonlinear Dynamics.